يصادف عيد منتصف الخريف اليوم الخامس عشر من الشهر الثامن من التقويم القمري الصيني.

لقرون ، شجع مهرجان منتصف الخريف على لم شمل الأسرة ، والأعياد الكبيرة والتمتع بالقمر الجميل. لكن بالنسبة للأشخاص في شيامن ، بدأت ألعابهم المثيرة للتو. ستقام لعبة "قمار كعكة القمر" المخصصة في كل مهرجان منتصف الخريف.

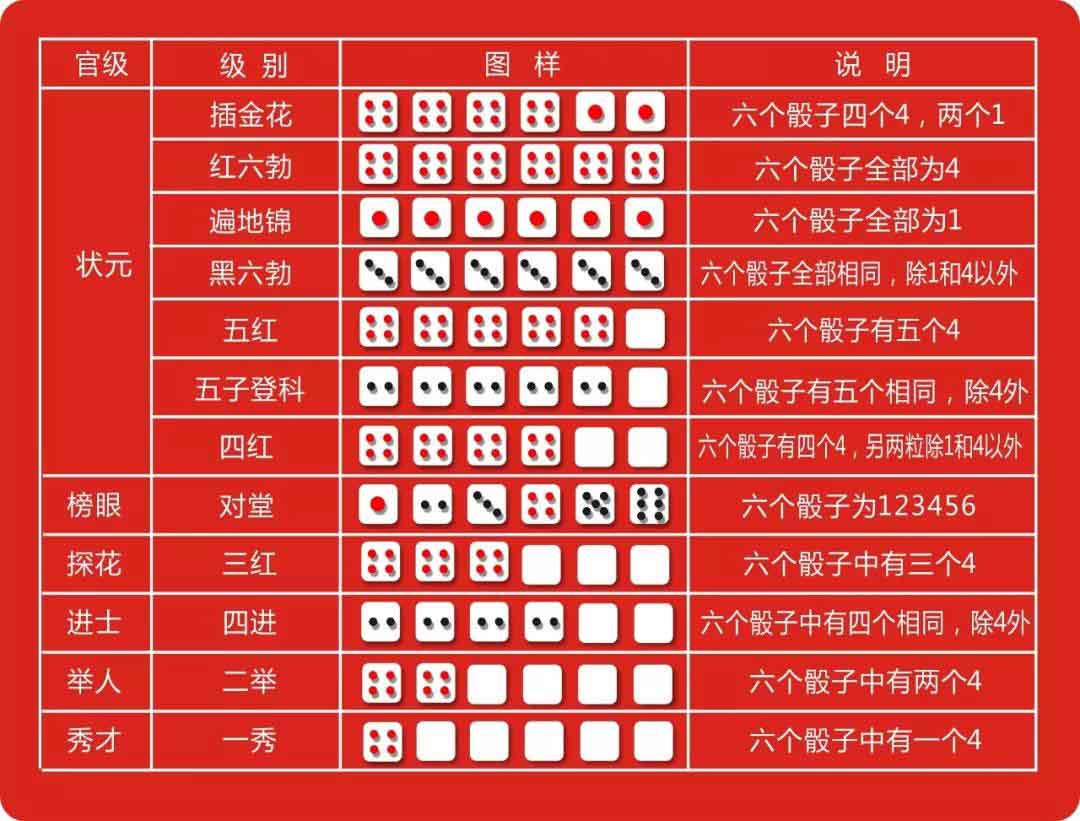
تجد حزمة من ستة نرد بالداخل بعد فتح كل صندوق من كعك القمر مزين بشكل مبهج.

القمار؟ صحيح ، لكنه قانوني بالتأكيد. لأن الرهانات بين السكان المحليين هي كعك القمر - وهكذا حصل هذا النشاط الاحتفالي الفريد على اسمه الصيني "بو بينج". يتم لعبها فقط حول مهرجان منتصف الخريف.

على الرغم من سهولة اللعب ، تحتوي الألعاب على قواعد معقدة للغاية يصعب تذكرها. لذلك من المفيد لبعض مصنعي كعك القمر طباعة القواعد على العبوة.

كل ما تتطلبه لعبة "Bo Bing" هو ستة نرد ووعاء صيني. ما عليك سوى رمي النرد في الوعاء - وستفوز بالنقاط المختلفة التي تحصل عليها للحصول على درجات مختلفة من الجوائز التي ستفوز بها.

عند المشي على طول الشوارع في هذه الجزيرة الصغيرة خلال هذا الوقت ، سوف تسمع الصوت الفضي اللطيف لدحرجة النرد. هتافات الفوز أو الخسارة في كل مكان.

يعود تاريخ لعب القمار على كعك القمر البالغ من العمر 300 عام إلى عهد أسرة تشينغ (1644-1911). وضع المخترع ، Zheng Chenggong (1624-62) ، وهو جنرال من أسرة Ming (1368-1644) ، جيشه في شيامن. كان تشنغ مصممًا على استعادة تايوان التي احتلها الغزاة الهولنديون منذ عام 1624.

عندما جاء كل مهرجان منتصف الخريف ، افتقد الجنود بطبيعة الحال عائلاتهم ، لكنهم قاتلوا بتصميم بطولي لطرد المعتدين.

ابتكر الجنرال تشنغ وضابطه الأدنى هونغ شو لعبة قمار كعك القمر للمساعدة في تخفيف الحنين إلى الوطن بين القوات.

تحتوي لعبة المقامرة على ست درجات من الجوائز ، والتي تم تسميتها على أنها الفائزين في الاختبارات الإمبراطورية القديمة ، وتحتوي على 63 كعكة قمر مختلفة الأحجام كجوائز.

من الأدنى إلى الأعلى ، ألقاب الرتب الستة هي Xiucai (الشخص الذي اجتاز الامتحان على مستوى المقاطعة) ، Juren (مرشح ناجح على مستوى المقاطعة) ، Jinshi (مرشح ناجح في أعلى اختبار إمبراطوري) ، Tanhua و Bangyan و Zhuangyuan (على التوالي هم رقم ثلاثة للفائزين رقم واحد في الامتحان الإمبراطوري بحضور الإمبراطور).

لاعبو اللعبة يرمون النرد بالتناوب. النقاط المختلفة التي يحسبونها تفوز للاعب "بلقب" ذي صلة ونوع مماثل من كعك القمر.

اللاعب المحظوظ الذي يحصل على النقاط ليجعله لقب "Zhuangyuan" سيكون الفائز الأكبر في اللعبة ، ويحصل على أكبر كعكة قمر.

في الصين القديمة ، كان الفوز بالامتحان الإمبراطوري هو السبيل الوحيد للدخول في مهنة رسمية كان حلم معظم المتعلمين ، منذ أن تم إنشاء نظام الامتحانات في عهد أسرة سوي (581-618 م).

لا عجب إذن ، إذا فاز شخص بـ "Zhuangyuan" من خلال الامتحان الإمبراطوري ، فإن النجاح سيحقق شرفًا كبيرًا له ولعائلته ، يليه منصب رفيع المستوى ومبلغ كبير من المال.

اللعبة لها علاقة بالرقم "أربعة". في لعبة Mooncake ، ترتبط النقاط لمعظم مراتب الجوائز بهذا الرقم.

على سبيل المثال ، يموت واحد من أربع نقاط يفوز بك "Xiucai" وأصغر كعك القمر. وإذا حصلت على أربعة نرد أو أكثر بأربع نقاط ، فتهانينا - ستفوز بـ "Zhuangyuan".

تقدم اللعبة 32 كعك قمر لـ "Xiucai" و 16 لـ "Juren" ويمكن استنتاج الباقي عن طريق القياس. لاعب واحد فقط سيفوز بلقب Zhuangyuan المحظوظ. هذا هو السبب في أن إجمالي 63 كعك القمر تم إعدادها للعبة.

باعتبارها لعبة تجمع بشكل جيد بين الثقافة والعادات الشعبية والترفيه ، سرعان ما أصبحت لعبة قمار كعكة القمر شائعة بين القوات.

لذلك وافق الجنرال تشنغ على أن يلعب الجنود اللعبة بالتناوب من الشهر الثالث عشر إلى الثامن عشر من الشهر الثامن حول عيد منتصف الخريف.

منذ ذلك الحين ، أصبح "Bo Bing" نشاطًا تقليديًا شائعًا بين السكان المحليين. في كل مهرجان منتصف الخريف ، يجتمع أفراد الأسرة للمقامرة كعك القمر ، في خضم الجدل حول الفائز.

كما ستنتج حلويات الكيك أنواعًا كثيرة من كعكات القمار لتلبية احتياجات السوق.

يعتقد الناس في شيامن أن الشخص الذي يفوز بـ "Zhuangyuan" في اللعبة ، سوف يحالفه الحظ في ذلك العام. ومهرجان منتصف الخريف هو ثاني عطلة هامة في شيامن إلى جانب عيد الربيع.

في الوقت الحاضر ، كعك القمر ليس النوع الوحيد من الجوائز. مع رفع مستوى معيشة الناس ، يمكن أيضًا كسب الضروريات اليومية والأجهزة المنزلية وحتى المال.

علاوة على ذلك ، يضيف الناس قواعد مضحكة. إذا كان النرد يقرأ الرقم "ستة" ، فانسى كل تلك الرتب المملة. أطفئ جميع الأنوار ، ثم اغتنم أكبر عدد ممكن من الجوائز في الظلام. إنها مزيج من الذاكرة الجيدة والسرعة العالية والجسم القوي.

جعلت تغييرات الجوائز اللعبة أكثر شعبية بين الأجيال الشابة.

القواعد على النحو التالي للاستدلال: